LEYES DE KEPLER

Las leyes de Kepler fueron enunciadas por Johannes Kepler para describir matemáticamente el movimiento de los planetas en sus órbitas alrededor del Sol.

Primera ley (1609)

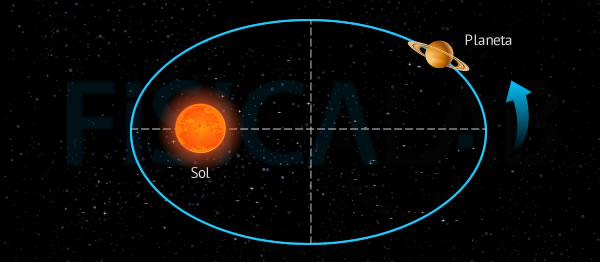
Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas. El Sol se encuentra en uno de los focos de la elipse.

 Los planetas describen órbitas elípticas estando el Sol en uno de sus focos

r₁ es la distancia más cercana al foco (cuando q=0) y r₂ es la distancia más alejada del foco (cuando q=p).

Una elipse es una figura geométrica que tiene las siguientes características:

• Semieje mayor a=(r₂+r₁)/2
• Semieje menor b
• Semidistancia focal c=(r₂-r₁)/2
• La relación entre los semiejes es a²=b²+c²
• La excentricidad se define como el cociente e=c/a=(r₂-r₁)/(r₂+r₁)

Segunda ley (1609)

El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.

La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.

L=mr₁·v₁=mr₂·v₂

Perihelio y afelio

• Perihelio: Es el punto de la órbita del planeta más próximo al Sol. La velocidad en las proximidades del perihelio es la máxima.
• Afelio: Es el punto de la órbita del planeta más lejano al Sol. La velocidad en las proximidades del afelio es la mínima.

Tercera ley (1618)

Para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.

${\displaystyle {\frac {T^{2}}{a^{3}}}=C={\text{constante}}}$

Donde, T  es el período orbital (tiempo que tarda en dar una vuelta alrededor del Sol), a  la distancia media del planeta con el Sol y C  la constante de proporcionalidad.

Estas leyes se aplican a otros cuerpos astronómicos que se encuentran en mutua influencia gravitatoria, como el sistema formado por la Tierra y el sol.